五大基础版块：
  一、代数基础：包括方程与不等式、函数与图像、数列与极限等，这些内容在竞赛中占据重要地位，要求学生熟练掌握并灵活应用。 

  二、几何与三角：涉及平面几何、立体几何以及三角函数的性质与应用等，要求学生具备良好的空间想象能力和逻辑推理能力。 

  三、数论与组合：数论是研究整数性质的数学分支，组合则关注离散结构的计数问题。这两部分内容在竞赛中常常出现，要求学生具备较高的抽象思维和创新能力。 

  四、应用题与建模：竞赛中常出现各种实际问题，要求学生运用数学知识进行建模和求解。这有助于学生将数学知识与实际问题相结合，提高解决问题的能力。 

  五、思维拓展与竞赛策略：除了具体的数学知识外，竞赛还注重培养学生的思维拓展能力和竞赛策略。学生需要学会如何快速分析问题、寻找突破口以及制定有效的解题策略。

八大核心理论：
  一、基础代数知识：包括一元一次方程、一元二次方程、不等式及其组、分式方程等，这些都是解决竞赛中代数问题的基本工具。

  二、几何知识：涵盖平面几何的基本概念，如点、线、面、角、三角形、四边形、圆等，以及它们的性质和定理。特别是三角形和圆的相关性质，是几何题目的重点。

  三、数论基础：包括整数的性质、质数与合数、最大公约数与最小公倍数、同余定理等，数论在数学竞赛中占有重要地位。

  四、概率与统计：基础的随机事件、概率计算、统计图表等，这些内容在竞赛中经常出现，尤其是在解决实际问题时的应用。

  五、函数与方程：函数的基本概念、性质、图像，以及方程的求解方法，包括函数图像的变换等。 

  六、逻辑推理与数学证明：数学竞赛中经常需要学生运用逻辑推理和数学证明来解决题目，包括直接证明、反证法、归纳法等。 

  七、数学建模：将实际问题转化为数学模型，运用数学方法来分析和解决问题。 

  八、综合应用能力：在竞赛中，学生需要将所学知识综合运用，解决一些综合性、创新性的问题。

九大高分技巧：
  一、掌握核心题型：初中数学竞赛通常围绕一些核心题型展开，例如反比例函数、几何证明、代数方程等。理解这些核心题型的解题思路和方法是至关重要的。 

  二、熟练运用公式和定理：确保对常用的数学公式和定理烂熟于心，这样在解题时可以迅速调用，提高解题效率。 

  三、练习逻辑推理：数学竞赛往往考查逻辑推理能力，通过大量练习，培养自己的逻辑思维和推理能力。 

  四、掌握解题策略：   

    1. 直接法：直接根据题目条件进行计算、推理或判断，得出答案。   

    2. 特殊值法：对于涉及字母取值范围的题目，可以选取特殊值代入原命题进行验证，以排除错误选项。   

    3. 淘汰法：将题目给出的选项逐一代入题干进行验证，淘汰错误的选项，直到找到正确答案。   

    4. 逐步淘汰法：在计算或推导过程中，逐步比较选项，淘汰不可能的选项，直至找到正确答案。   

    5. 数形结合法：将数学问题的代数含义和几何意义结合起来，利用图形来帮助理解和解题。 

  五、合理分配时间：在竞赛中，时间是非常宝贵的。要学会合理分配时间，对于难题不要死磕，先做自己会做的题目，确保拿到这些题目的分数。 

  六、注意审题：仔细审题，避免因为读题不清或理解错误而失分。 

  七、练习历年真题：通过练习历年的数学竞赛真题，了解竞赛的题型和难度，增强自己的应试能力。 

  八、培养良好的心态：保持冷静和自信，遇到难题时不要慌乱，相信自己能够解决。 

  九、团队合作：在竞赛中，如果允许团队合作，要充分利用团队的力量，互相讨论和帮助，共同解决问题。

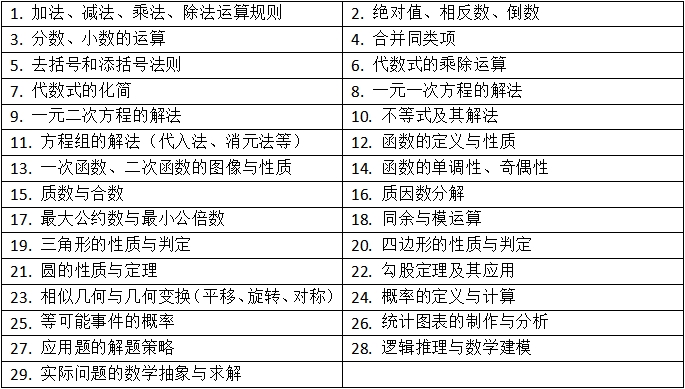
29个必背考点：